當大數(shù)據(jù)席卷各行各業(yè)，控制理論也迎來新的拐點：從依賴模型到依賴數(shù)據(jù)。

但是，在數(shù)據(jù)驅(qū)動控制領(lǐng)域，卻缺乏一種標準化的數(shù)據(jù)表示形式。

針對這一問題，清華大學李升波教授課題組（iDLab）首次將現(xiàn)代控制理論中的標準型概念引入數(shù)據(jù)驅(qū)動控制（datatic control）范式，提出了一種基于數(shù)據(jù)的系統(tǒng)描述新形式。

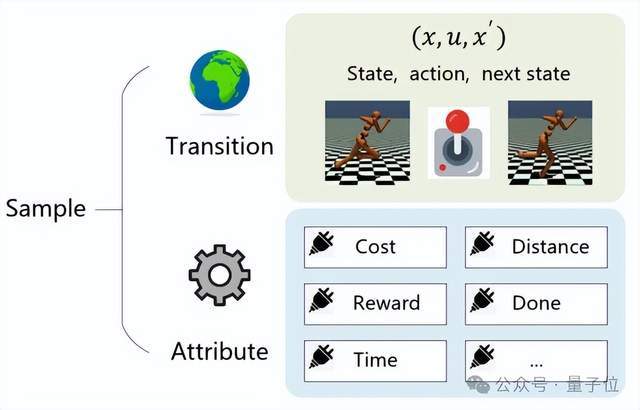
每個標準形式的樣本由必要的轉(zhuǎn)移和可插拔的屬性組成，分別用于描述系統(tǒng)變化規(guī)律和人為定義特征。

不僅如此，該數(shù)據(jù)標準型還可根據(jù)算法需求定制屬性，顯著加速控制器設(shè)計，為提高數(shù)據(jù)驅(qū)動算法效率提供了新的思路。

目前，該成果已發(fā)表于ACC2025。

從模型標準型到數(shù)據(jù)標準型

人工智能的蓬勃發(fā)展，離不開數(shù)據(jù)這一核心支柱。

近年來，隨著人工智能技術(shù)的廣泛應(yīng)用，以數(shù)據(jù)為核心的系統(tǒng)表征方法迅速滲透到控制領(lǐng)域。

控制系統(tǒng)的設(shè)計方法正迎來一場從模型驅(qū)動向數(shù)據(jù)驅(qū)動的范式變革，即從傳統(tǒng)的模型驅(qū)動控制（modelic control，即model-driven control）到數(shù)據(jù)驅(qū)動控制（datatic control，即data-driven control）。

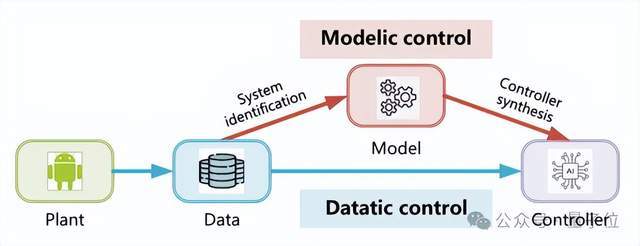
圖1：兩種控制范式對比

模型驅(qū)動控制（上方路徑）首先利用系統(tǒng)辨識來擬合一個模型，然后用這個模型來合成控制器。

數(shù)據(jù)驅(qū)動控制（下方路徑）則直接利用數(shù)據(jù)來求解控制器。

在模型驅(qū)動控制（modelic control）的范式下，模型的標準型是一個有力工具。

例如，現(xiàn)代控制理論的奠基人魯?shù)婪?middot;卡爾曼（Rudolf E. Kálmán）指出：將狀態(tài)空間模型表示為可控標準型或可觀標準型，無需額外的判斷步驟即可直接確保系統(tǒng)的可控性或可觀性。

此外，現(xiàn)代群論的奠基人之一卡米耶·若爾當（Camille Jordan）指出：任何狀態(tài)空間模型都可以轉(zhuǎn)換為約旦標準型，系統(tǒng)矩陣會變?yōu)閷欠疥嚕鋵蔷€元素代表系統(tǒng)的特征值。

因此，只需檢查所有特征值是否為負，即可輕松驗證系統(tǒng)的穩(wěn)定性。更進一步，不同的特征值對應(yīng)著系統(tǒng)不同的模態(tài)，這使得控制器設(shè)計更具針對性。

數(shù)據(jù)驅(qū)動控制（datatic control）范式下的標準型是一個新問題。

近年來，隨著機器人、自動駕駛等具身智能系統(tǒng)的蓬勃發(fā)展，海量、復雜的交互數(shù)據(jù)正以前所未有的速度被生成。這不僅為傳統(tǒng)控制算法帶來了巨大挑戰(zhàn)，也引出了一個全新的議題：

在數(shù)據(jù)驅(qū)動控制范式下，如何構(gòu)建一個有效利用大規(guī)模數(shù)據(jù)的標準描述方式？即是否存在數(shù)據(jù)驅(qū)動版本的標準型？

數(shù)據(jù)的描述形式直接決定了后續(xù)控制器設(shè)計算法的運行效率和可擴展性。

以強化學習為例，訓練算法通常涉及大量的迭代計算和高維數(shù)據(jù)處理。

在這一過程中，算法很容易陷入重復計算的泥潭，例如在每一步訓練迭代中，都重新計算樣本間的范數(shù)距離、特征相似度等信息。

這種重復性的計算不僅耗時，而且對計算資源造成了顯著的浪費，嚴重制約了算法在現(xiàn)實世界中的部署和應(yīng)用。

因此，如何高效、標準地組織和描述數(shù)據(jù)，以減少冗余計算、加速算法運行，是數(shù)據(jù)驅(qū)動控制范式面臨的一項核心挑戰(zhàn)。

類比于模型標準型，該研究首次提出，適用于數(shù)據(jù)驅(qū)動控制系統(tǒng)的標準描述形式：每條樣本數(shù)據(jù)包含兩個部分（如圖2所示）：